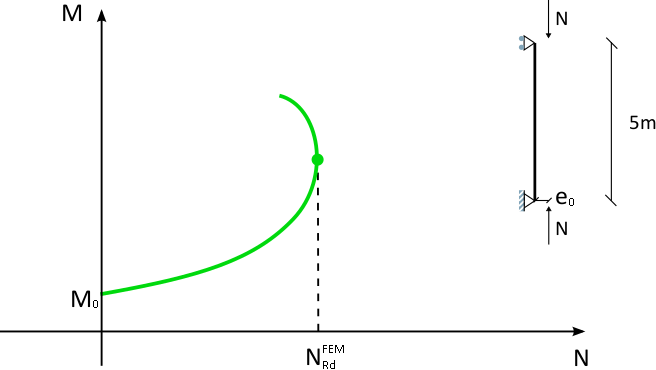
Confronto dei metodi per la valutazione degli effetti locali del secondo ordine
Al fine di valutare l’efficacia dei metodi proposti per la valutazione degli effetti del secondo ordine locali, sono stati confrontati i risultati ottenuti in termini di carico assiale resistente di una medesima “colonna modello” assunta come riferimento. Gli approcci considerati sono:
1. metodo della “rigidezza nominale” come definito in EC2 § 5.8.7;
2. metodo della “curvatura nominale” come definito in EC2 § 5.8.8;
3. metodo generale, basato sull’analisi non lineare, come definito in EC2 § 5.8.6 ed eseguito con l’ausilio del software SAP2000.
Il caso studio è rappresentato da una colonna isolata, di sezione 30 x 30 cm ed altezza libera pari a 5 metri soggetta a sforzo normale eccentrico lungo un’asse principale. l’eccentricità del carico è stata assunta costante e pari al valore corrispondente alle imperfezioni geometriche come definite al § 5.2(7) dell’EC2:
\( e_0 = l_0/400 \)
La stima del carico ultimo attraverso i metodi semplificati è stata effettuata calcolando il momento sollecitante totale corrispondente a valori di sforzo assiale crescenti fino al raggiungimento del dominio resistente del pilastro, determinato in accordo alle prescrizioni del § 6.1 dell’EC2 (Figura 12). Viceversa, la capacità della colonna per mezzo dell’analisi non lineare è stata fissata sulla base delle curve N-M ottenute applicando l’azione assiale eccentrica in controllo di spostamento (Figura 13).
Figura 12: determinazione del carico ultimo della colonna modello mediante metodi semplificati.
a) Metodo della rigidezza nominale – b) Metodo della curvatura nominale
Figura 12: determinazione del carico ultimo della colonna modello mediante analisi non lineare
Allo scopo di valutare l’influenza della classe del calcestruzzo e del quantitativo d’armatura, i test sono stati ripetuti per due diversi calcestruzzi e due layout di armatura. Gli effetti della viscosità sono stati introdotti considerando un tempo di maturazione, \( t_0 \), pari a 28 giorni e un rapporto fra carichi in combinazione quasi permanente e carichi allo SLU pari a 0.62.
Tutte le configurazioni testate sono riportate nella seguente tabella.
 Per la valutazione dei risultati sono stati presi come riferimento i valori ottenuti attraverso l’analisi non lineare. L’approccio secondo il metodo della “rigidezza nominale” ha mostrato un ottimo accordo con il metodo generale, risultando sempre in favore di sicurezza con una sottostima media del carico resistente pari a circa il 7%. Viceversa, il carico ultimo calcolato attraverso il metodo della “curvatura nominale” è risultato sempre ampiamente maggiore di quello calcolato mediante analisi non lineare, con una sovrastima media di più del 25%.
Per la valutazione dei risultati sono stati presi come riferimento i valori ottenuti attraverso l’analisi non lineare. L’approccio secondo il metodo della “rigidezza nominale” ha mostrato un ottimo accordo con il metodo generale, risultando sempre in favore di sicurezza con una sottostima media del carico resistente pari a circa il 7%. Viceversa, il carico ultimo calcolato attraverso il metodo della “curvatura nominale” è risultato sempre ampiamente maggiore di quello calcolato mediante analisi non lineare, con una sovrastima media di più del 25%.
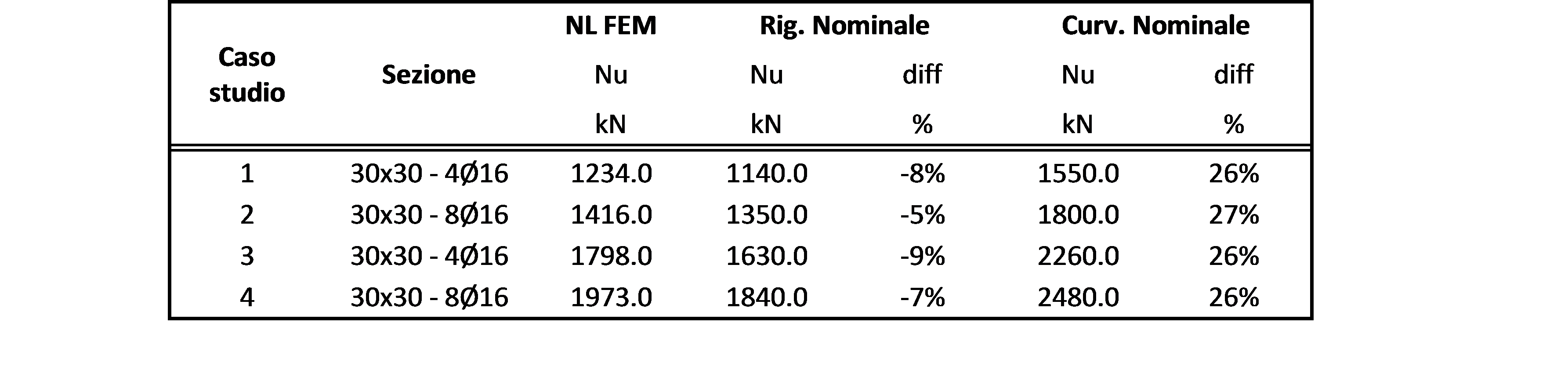 Lo stesso confronto è stato ripetuto per un’altra colonna avente le medesime caratteristiche ma con luce libera inferiore, pari a 3 metri. In questo caso entrambi i metodi semplificati hanno prodotto risultati leggermente in sfavore di sicurezza con una sovrastima media del carico ultimo pari all’8% per il metodo della “rigidezza nominale” e pari all’11% per il metodo della “curvatura nominale”.
Lo stesso confronto è stato ripetuto per un’altra colonna avente le medesime caratteristiche ma con luce libera inferiore, pari a 3 metri. In questo caso entrambi i metodi semplificati hanno prodotto risultati leggermente in sfavore di sicurezza con una sovrastima media del carico ultimo pari all’8% per il metodo della “rigidezza nominale” e pari all’11% per il metodo della “curvatura nominale”.
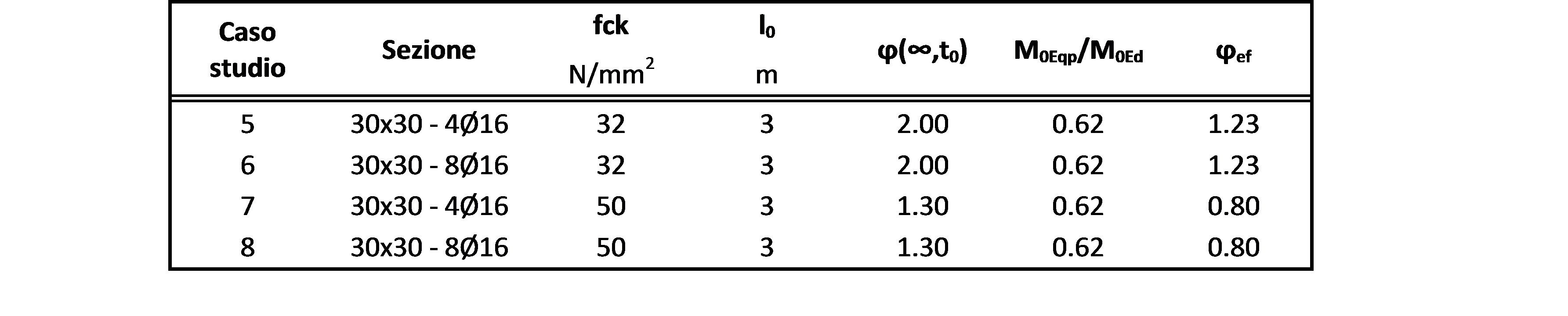
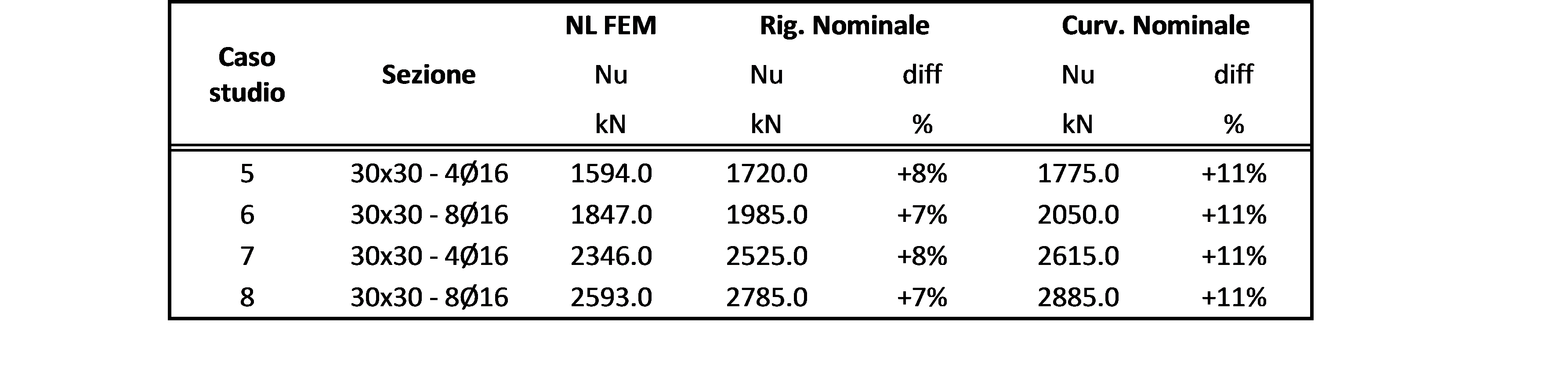 Esaminando i risultati grafici dettagliati (riportati nelle figure sottostanti) appare evidente come il metodo della “rigidezza nominale” sia risultato più accurato nel predire il comportamento di tutte le configurazioni testate, sia con riferimento alla colonna snella che alla colonna tozza. Inoltre, tale metodo ha prodotto risultati in favore di sicurezza per quasi tutti i range di sforzo assiale ammissibili. Il metodo della “curvatura nominale”, al contrario, è risultato sempre eccessivamente conservativo per bassi valori di sforzo assiale diventando poi in sfavore di sicurezza al crescere di \( N \). Entrambi i metodi semplificati hanno sovrastimato leggermente la capacità resistente della colonna tozza per alti valori di carico assiale.
Esaminando i risultati grafici dettagliati (riportati nelle figure sottostanti) appare evidente come il metodo della “rigidezza nominale” sia risultato più accurato nel predire il comportamento di tutte le configurazioni testate, sia con riferimento alla colonna snella che alla colonna tozza. Inoltre, tale metodo ha prodotto risultati in favore di sicurezza per quasi tutti i range di sforzo assiale ammissibili. Il metodo della “curvatura nominale”, al contrario, è risultato sempre eccessivamente conservativo per bassi valori di sforzo assiale diventando poi in sfavore di sicurezza al crescere di \( N \). Entrambi i metodi semplificati hanno sovrastimato leggermente la capacità resistente della colonna tozza per alti valori di carico assiale.
 Figura 14: sezione 30×30 | \( f_{ck}=32 \) | \( 4 \phi 16 \) | \( L_0 = 5m \) | \( \varphi_{ef} = 1.23 \)
Figura 14: sezione 30×30 | \( f_{ck}=32 \) | \( 4 \phi 16 \) | \( L_0 = 5m \) | \( \varphi_{ef} = 1.23 \)
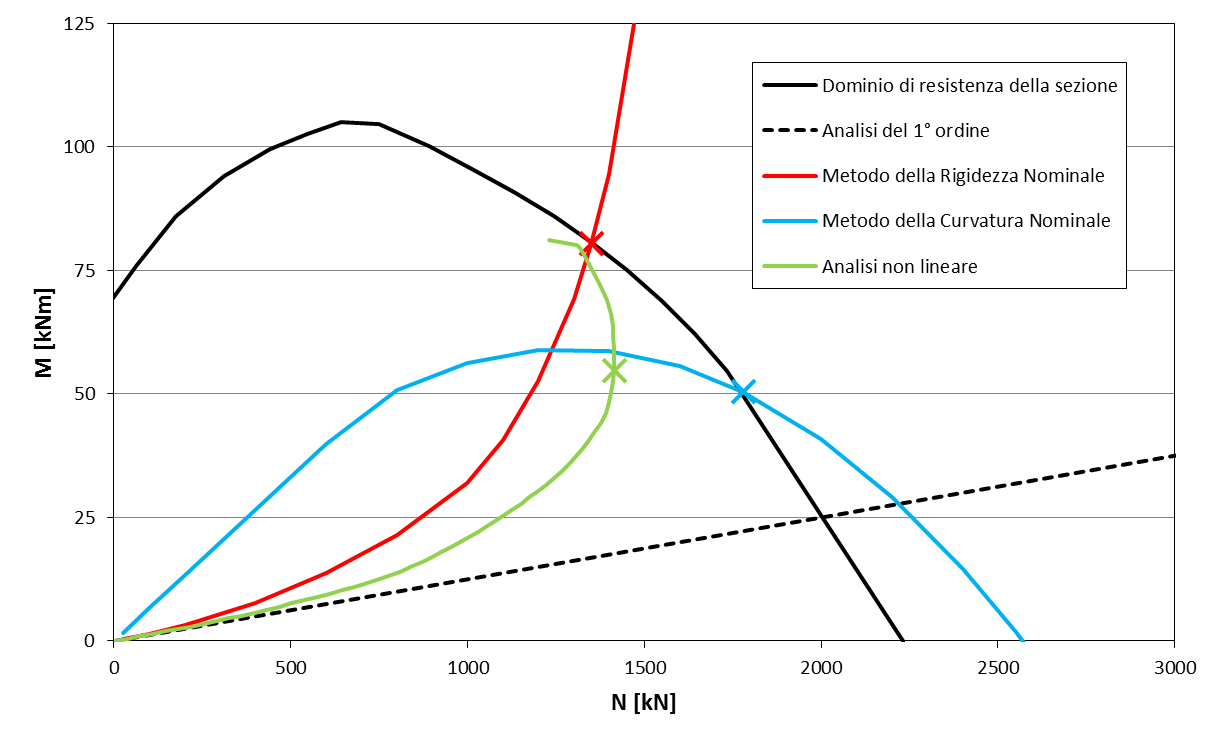 Figura 15: sezione 30×30 | \( f_{ck}=32 \) | \( 8 \phi 16 \) | \( L_0 = 5m \) | \( \varphi_{ef} = 1.23 \)
Figura 15: sezione 30×30 | \( f_{ck}=32 \) | \( 8 \phi 16 \) | \( L_0 = 5m \) | \( \varphi_{ef} = 1.23 \)
 Figura 16: sezione 30×30 | \( f_{ck}=50 \) | \( 4 \phi 16 \) | \( L_0 = 5m \) | \( \varphi_{ef} = 0.80 \)
Figura 16: sezione 30×30 | \( f_{ck}=50 \) | \( 4 \phi 16 \) | \( L_0 = 5m \) | \( \varphi_{ef} = 0.80 \)
 Figura 17: sezione 30×30 | \( f_{ck}=50 \) | \( 8 \phi 16 \) | \( L_0 = 5m \) | \( \varphi_{ef} = 0.80 \)
Figura 17: sezione 30×30 | \( f_{ck}=50 \) | \( 8 \phi 16 \) | \( L_0 = 5m \) | \( \varphi_{ef} = 0.80 \)
 Figura 18: sezione 30×30 | \( f_{ck}=32 \) | \( 4 \phi 16 \) | \( L_0 = 3m \) | \( \varphi_{ef} = 1.23 \)
Figura 18: sezione 30×30 | \( f_{ck}=32 \) | \( 4 \phi 16 \) | \( L_0 = 3m \) | \( \varphi_{ef} = 1.23 \)
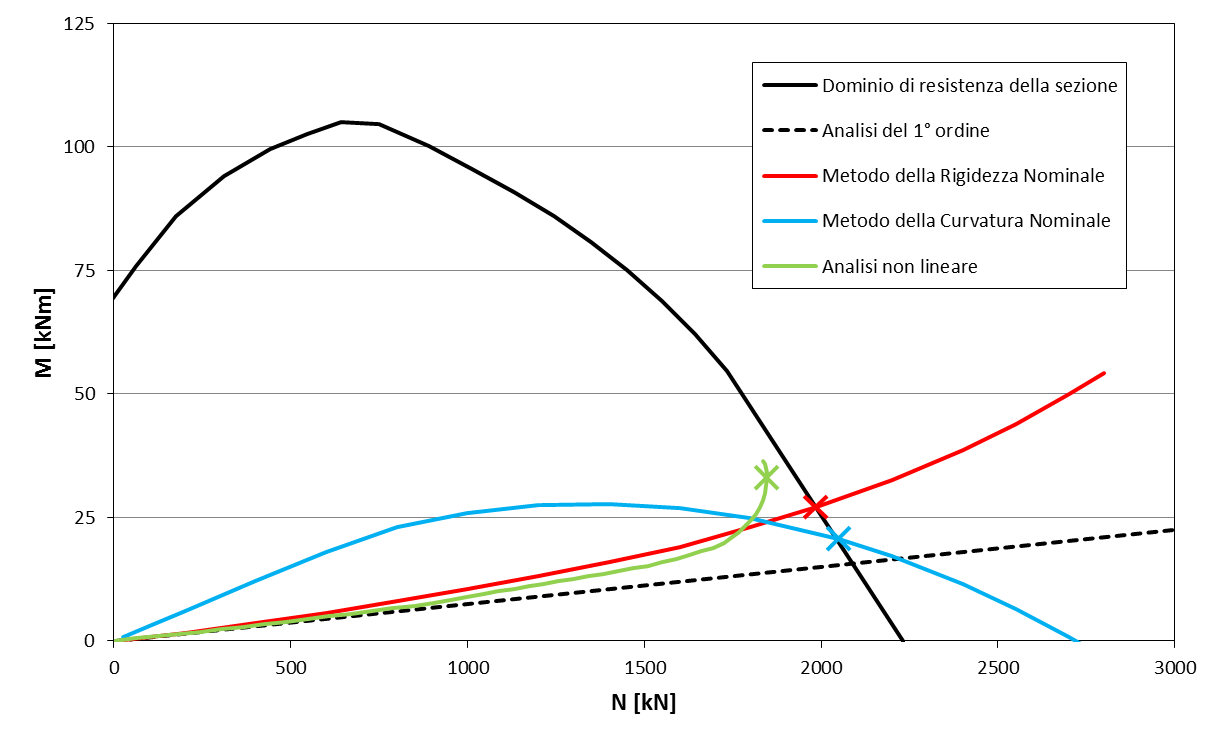 Figura 19: sezione 30×30 | \( f_{ck}=32 \) | \( 8 \phi 16 \) | \( L_0 = 3m \) | \( \varphi_{ef} = 1.23 \)
Figura 19: sezione 30×30 | \( f_{ck}=32 \) | \( 8 \phi 16 \) | \( L_0 = 3m \) | \( \varphi_{ef} = 1.23 \)
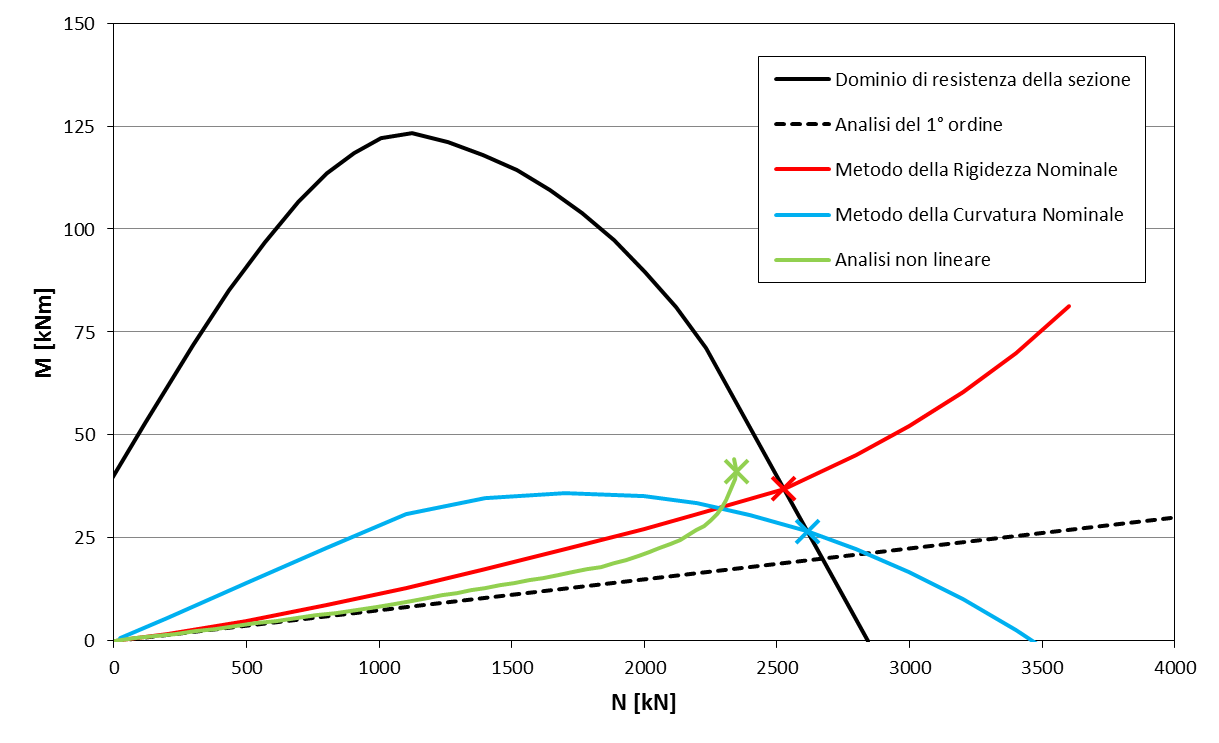 Figura 20: sezione 30×30 | \( f_{ck}=50 \) | \( 4 \phi 16 \) | \( L_0 = 3m \) | \( \varphi_{ef} = 0.80 \)
Figura 20: sezione 30×30 | \( f_{ck}=50 \) | \( 4 \phi 16 \) | \( L_0 = 3m \) | \( \varphi_{ef} = 0.80 \)
 Figura 21: sezione 30×30 | \( f_{ck}=50 \) | \( 8 \phi 16 \) | \( L_0 = 3m \) | \( \varphi_{ef} = 0.80 \)
Figura 21: sezione 30×30 | \( f_{ck}=50 \) | \( 8 \phi 16 \) | \( L_0 = 3m \) | \( \varphi_{ef} = 0.80 \)
| Indietro | Prosegui |
|---|